1. Einführung

Matrix-Anpassung ist ein Verfahren zum Anpassen einer a priori OD-Matrix unter Verwendung von Verkehrszählungen von Detektoren, Detektorstationen, Straßenabschnitten oder Kurven von Knoten oder Superknoten. Der Lösungsalgorithmus basiert auf einem zweistufigen Modell, das heuristisch durch einen gradientenbasierten Algorithmus gelöst wird, der eine Zuweisung bei jeder Iteration ausführt. Der Algorithmus berechnet eine Sequenz von OD-Matrizen, die nacheinander den kleinsten Quadratfehler zwischen den Verkehrszählungen von Detektoren und Verkehrsflüssen reduzieren, die durch eine Verkehrszuweisung erhalten werden.

Der Algorithmus, der zur Lösung des Problems verwendet wird, ist heuristischer Natur, vom steilsten Abstiegstyp, und garantiert kein globales Optimum für das formulierte Problem, so dass manuelles Eingreifen manchmal notwendig ist, um ein gutes Ergebnis zu erzielen.

Aimsun Next bietet mehrere Optionen, um den Anpassungsprozess zu begrenzen, um überzupassende anpassungen zu verhindern und so nah wie die ursprüngliche Matrix zu bleiben, z. B.: Matrixelastizität und Triplängenverteilungselastizität können so eingestellt werden, dass jede Änderung von der ursprünglichen Matrix global begrenzt wird; oder in einigen Fällen kann eine maximale Abweichungsmatrix bereitgestellt werden, um für jedes einzelne OD-Paar eine Änderungsgrenze genau festzulegen; oder die Gewichtsfunktion kann verwendet werden, um den beobachteten Werten (realen Daten), die für die Anpassung verwendet werden, unterschiedliche Gewichtungen zuzuweisen.

Die Verwendung der Gewichtsfunktion ist die am wenigsten erforschte dieser Optionen. Die Gewichtsfunktion ist die einzige Option, die die beobachteten Werte direkt beeinflusst, und darüber hinaus ist ein bekanntes Problem des Fehlers der kleinsten Quadrate, dass sie hohe Werte bevorzugt. Die Gewichtsfunktion, wenn sie richtig verwendet wird, könnte das Ungleichgewicht zwischen hohen und niedrigen Anzahlen verringern und somit das Gesamtanpassungsergebnis verbessern.

In diesem technischen Hinweis werden die Auswirkungen der Gewichtsfunktion auf den Matrixanpassungsprozess untersucht.

2. Test model and data

Die Basisnachfrage für die OD-Anpassung wird aus dem strategischen Modell in Emmeabgeleitet. Die in dieser Studie verwendeten Detektordaten stammen aus zwei verschiedenen Quellen: den Autobahndaten, die von den Autobahndetektoren erfasst werden und die die Anzahl der einzelnen Fahrzeuge alle 3 Minuten aufzeichnen. Der größte Teil der signalisierten Kreuzung hat Schnittmengen, die aus der historischen SCATS-Datenbank gesammelt wurden. SCATS-Daten werden im 1-5-Minuten-Takt gespeichert. Das kombinierte Dataset wurde im 15-Minuten-Takt aktualisiert. Diese Detektordaten werden später mit Detektorstationsdaten kombiniert (eine Detektorstation auf einem mehrspurigen Straßenabschnitt ist eine Sammlung von Detektoren mit einer gemeinsamen Fahrtrichtung).

Das Modell umfasst lokale Straßen zu Schnellstraßen und verfügt über insgesamt 1.236 Melderstationen, von denen 203 auf Autobahnen liegen, und der Rest an städtischen signalisierten Kreuzungen. Das Ausmaß des an verschiedenen Detektoren beobachteten Durchflusses reicht von 0 – 6.070 veh/hr.

3. Auswirkungen der Gewichtsfunktion auf die Matrixanpassung

3.1 Gewichtsfunktion

Eine Einstellgewichtsfunktion kann als Form der Zuverlässigkeit der realen Daten (Abschnitts-/Detektor-/Drehzahlen) verwendet werden, die für den Einstellprozess verwendet werden. Standardmäßig wird keine Gewichtsfunktion angewendet. In dieser Studie wurden folgende Gewichtsfunktionen angewendet:

Gewichtsfunktion 1 = (1/(beobachtetes Volume 0,2)*10
Gewichtsfunktion 2 = (1/(beobachtetes Volume 0,4)*50
Gewichtsfunktion 3 = (1/(beobachtetes Volume 0,6)*300

3.2 Auswirkungen der Gewichtsfunktion auf die OD-Anpassungsleistung

Um den Effekt der Gewichtsfunktion auf die Matrixanpassung zu verstehen, nehmen wir vier verschiedene statische OD-Anpassungen: ohne Gewichtsfunktion und mit der Gewichtsfunktion 1, 2 und 3. Die Experimente hatten die folgenden Einstellungen:

• Anzahl der äußeren Iterationen = 20
• Anzahl der Gradientenabstiegsiterationen = 3
• Anzahl der inneren Iterationen = 50
• Relativer Abstand = 0,1
• Zuweisungsmethode = Konjugat Frank und Wolfe

Tabelle 1 zeigt das Ergebnis der Matrixanpassungsexperimente. Die Leistung der Anpassung wird mit dem beobachteten und simulierten Durchfluss validiert. Die Hauptkriterien für die Validierung sind GEH <5, durchschnittliche GEH-Stufe und Regression R2.

Tabelle 1 zeigt, dass die Matrixanpassung auch ohne Gewichtsfunktion eine gute Arbeit leistet. Die GEH <5 für alle Daten beträgt etwa 61, während bei beobachteten Strömungen über 2000 100. Ein bekanntes Problem der Matrixanpassung ist, dass sie einen hohen Durchfluss begünstigt, da der Algorithmus den kleinsten Quadratfehler zwischen den Verkehrszählungen von Detektoren und Verkehrsflüssen verwendet, die durch eine Verkehrszuweisung erhalten werden. Wenn wir also eine Gewichtsfunktion verwenden, die kleinen Anzahlen ein hohes Gewicht verleiht, ist es wahrscheinlich, dass die Anpassungsleistung verbessert wird. Tabelle 1 zeigt, dass die Verwendung von Gewicht 3 die Gesamt-GEH <5 bis 76 verbessert. Die Gewichtsfunktion hat den durchschnittlichen GEH-Wert reduziert.

Interessanterweise hat der durchschnittliche GEH für den beobachteten Fluss über 2000 mit der Gewichtszunahme zugenommen, während das Gegenteil für den Fluss unter 2000 beobachtet wird. Dieses Verhalten wird durch die Art der in dieser Studie verwendeten Gewichtsfunktion verursacht, die den kleinen Strömen größeres Gewicht beimaß. Daher zeigte die angepasste Matrix eine bessere Leistung für lokale Straßen, d.h. Straßen mit Durchfluss <2000 veh/hr.

Die Anwendung der Gewichtsfunktion verbessert deutlich die Anpassungsleistung. Die Gewichtsfunktion wird jedoch wahrscheinlich mehr Verzerrungen in der ursprünglichen Matrix verursachen als die Anpassung ohne Gewichtsfunktion. Die folgende Abbildung zeigt z. B. die Matrixverzerrung durch das Streudiagramm des angepassten vs. ursprünglichen Bedarfs an. Der Regressions-R2-Wert für keine Gewichtung und Gewicht 3 beträgt 0,8143 bzw. 0,7138. Die Verwendung von Gewicht 3 erzeugte mehr Verzerrungen in der ursprünglichen Matrix, um den beobachteten Fluss genauer zu entsprechen.

Die Art der Gewichtsfunktion wirkt sich auf die Verteilung der Reiselänge aus. In dieser Studie begünstigt die Gewichtsfunktion beispielsweise kleine Ströme, die wahrscheinlich auf lokalen Straßen auftreten. Daher erzeugt eine Funktion mit hohem Gewicht mehr kurze Fahrten als keine Gewichtsfunktion (siehe folgende Abbildung).

Aus der obigen Diskussion geht klar hervor, dass die Gewichtsfunktion ein leistungsfähiges Werkzeug zur Matrixanpassung ist. Es besteht jedoch die Gefahr, dass das Modell überfordert ist. Ein Gleichgewicht zwischen den unteren und hohen Durchflussbereichen des Netzes sollte durch Auswahl einer geeigneten Gewichtsfunktion beibehalten werden.

Abbildung 4: Auswirkungen der Gewichtsfunktion auf Matrixverformung und Federlängenverteilung

3.3 Auswirkungen der Gradientenabstiegsiteration auf die OD-Anpassungsleistung

Im zweistufigen Optimierungsframework für die Matrixanpassung in Aimsun Next wird die Gradientenabstiegsmethode ausgeführt, ohne die Pfadauswahlergebnisse zu ändern, die aus der statischen Zuweisung stammen, die bei der äußeren Iteration ausgeführt wurde. Eine Iteration mit höherem Gradientenabstieg sollte die Matrixanpassung mit den Kosten einer höheren Laufzeit verbessern. Im vorherigen Test haben wir eine Gradientenabstiegsiteration von 3 verwendet. In diesem Abschnitt werden wir die Auswirkungen der Gradientenabstiegsiteration auf die Matrixanpassungsleistung ohne Gewicht als Basisfall beobachten. Tabelle 2 zeigt den Effekt der Verlaufsabstiegsiteration auf die Matrixanpassungsleistung. Es wurde keine Gewichtsfunktion verwendet.

Eine genaue Beobachtung der Veränderungen im Durchschnitt GEH oder GEH< 5 zeigt eine schnelle Veränderung der Matrixanpassungsleistung zwischen Iteration S. 1 und 3. Die Änderungen der Anpassungsleistung von Dergradientenabstiegsiteration 3 bis 9 sind fast linear. Daher wurde in der restlichen Analyse eine Gradientenabstiegsiteration = 3 verwendet.

Die Verbesserung der Matrixanpassung kommt mit einer höheren Verformung der ursprünglichen Nachfrage- und Fahrtlängenverteilung. In Abbildung 6 wird ein Vergleich der Matrixverformung und der Triplängenverteilung zwischen Dergradientenabstiegiteration 1 und 7 dargestellt. Die Regression R2 wurde auf 0,77 mit 7 Gradientenabstiegsiteration im Vergleich zu einem R2-Wert von 0,88 mit nur 1 Gradientenabstiegsiteration reduziert. In ähnlicher Weise wird eine höhere Anzahl von Kurztrips mit der Zunahme der Gradientenabstiegsiteration beobachtet.

4. Auswirkungen der Gewichtsfunktion auf matrixverzerrung

Bisher wurde die Analyse an realen Daten durchgeführt, die aus verschiedenen Quellen erhoben wurden. Die Basisnachfrage stammt aus einem strategischen Modell. Da die für die Anpassung verwendeten Daten aus verschiedenen Quellen stammen, ist es schwierig zu wissen, welche zuverlässiger ist. Durch die Auferlegung eines unterschiedlichen Gewichts oder die Steuerung anderer Parameter erzeugt der Anpassungsprozess einen Ausgang, der von der Input-(Basis-)Matrix verzerrt wurde, um die Anzahlen anzupassen. Wir haben jedoch keine Ahnung, wie nah das Anpassungsergebnis an der wahren Matrix ist. True Matrix ist eine hypothetische Matrix, die (wenn verfügbar) die gleichen Detektorzahlen erzeugen würde.

In diesem Abschnitt haben wir einen hypothetischen Test durchgeführt, um zu beobachten, ob die Gewichtsfunktion hilft, eine Bedarfsmatrix zu erzeugen, die der tatsächlichen Nachfrage nahe kommt. Wir haben beobachtet, dass die Gewichtsfunktion eine bessere Leistung für die Matrixanpassung bietet. Die bessere Leistung bringt jedoch die Kosten einer höheren Verformung der Eingangsmatrix und höhere Änderungen in der Triplängenverteilung mit sich. Es wäre interessant zu wissen, ob diese Veränderungen eine Matrix hervorgebracht haben, die näher an der wahren Matrix ist. Wenn das Ergebnis näher an der wahren Matrix liegt, sollten die höheren Verformungen zur Eingabematrix akzeptabel sein.

4.1 Schaffung von echter und synthetischer Nachfrage und RDS aus der wahren Nachfrage

Wir haben den angepassten Bedarf aus Abschnitt 3.2 mit Gewichtsfunktion 3 (da er die besten Einstellleistungen erzeugte) übernommen. Wir haben diese Forderung als „wahre Forderung“ verstanden. Der Gleichgewichtsfluss, der aus diesem tatsächlichen Bedarf an den Detektorstationen erzeugt wird, wird als das wahre RDS bezeichnet. Dieses echte RDS ist ein perfektes RDS, das frei von Beobachtungsfehlern ist, und der gesamte Detektorfluss stimmt mit den vorgelagerten, nachgeschalteten Strömungen sowie zwischen allen anderen Ansätzen eines Schnittpunkts überein.

Die tatsächliche Nachfrage wurde durch Hinzufügen eines weißen Rauschens verzerrt und als „synthetische Nachfrage“ bezeichnet, die für die Matrixanpassung verwendet wird. Das weiße Rauschen wird aus einer Normalverteilung mit Mittelwert = 0 und Standardabweichung = 0,5, Saatgut = 1 erzeugt. Der synthetische Bedarf wird nach folgender Formel erstellt: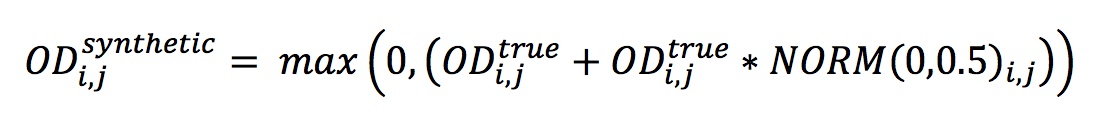

Wobei i bzw. j Herkunft bzw. Bestimmung bezeichnen.

In der realen Welt haben wir keinen Zugang zu dieser „wahren Nachfrage“. Wir werden nur Zugang zur „synthetischen Nachfrage“ haben. Daher wird dieser Test einige wertvolle Einblicke in die Nähe der Anpassung liefern, um die Matrix an die ursprüngliche/wahre Nachfrage heranzuführen.

4.2 OD-Anpassungsergebnis mit synthetischer Nachfrage und echtem RDS

Tabelle 3 zeigt das Ergebnis der Anpassung mit synthetischer Nachfrage und echter RDS. Wie wir schon vor der Gewichtsfunktion beobachtet hatten, hat das gut funktioniert. Auch ohne Die Gewichtsfunktion ist das Ergebnis gut. Der Grund ist höchstwahrscheinlich auf die Qualität von RDS zurückzuführen. Da das RDS frei von Inkonsistenzen im Durchfluss ist, hatte der Anpassungsprozess weniger Schwierigkeiten, globale Minima zu finden.

Da wir nun sowohl Aufdiebe auf die wahre als auch auf die synthetische Matrix haben, können wir die Qualität der angepassten Matrix vergleichen. Tabelle 4 zeigt die Regressions-R2-Werte zwischen dem angepassten und dem tatsächlichen Bedarf. Es zeigt auch die RegressionS-R2-Werte zwischen dem angepassten und dem synthetischen Bedarf.

Die Gewichtsfunktion hat mehr Verformung der synthetischen Matrix erzeugt, die für die Anpassung verwendet wurde (die Regression R2 zwischen synthetischem und angepasstem Bedarf ist die niedrigste für Gewichtsfunktion 3 und die höchste für keinen Gewichtsfall). Interessanterweise wird das Gegenteil für die wahre Nachfrage beobachtet. Diese hohe Verformung hat die Matrix näher an die wahre Matrix gebracht. Die Regression R2 zwischen dem angepassten und dem tatsächlichen Bedarf ist die höchste für Gewichtsfunktion 3 und die niedrigste für keinen Gewichtenfall. Es liegt auf der Hand, dass die Gewichtsfunktion die Matrix in die richtige Richtung verformt hat, um einen angepassten Bedarf zu erzeugen, der den tatsächlichen Bedarf genau darstellt.

5. Zusammenfassung

• Die Verwendung der Anpassungsgewichtsfunktion kann die Matrixanpassungsleistung deutlich verbessern.
• In den meisten Projektzielen geht es darum, einen hohen GEH <5 Prozent zu erreichen. Der normale Einstellvorgang maximiert den R2-Wert, hat jedoch keine Kontrolle über den GEH.
• Diese Studie findet einen engen Zusammenhang zwischen der Gewichtsfunktion und GEH. Die Erhöhung der Gewichtsfunktion hat dazu beigetragen, das durchschnittliche GEH-Niveau zu senken und den <GEH 5 Prozent zu erhöhen.
• Die Gewichtsfunktion erzeugt eine höhere Verformung der Basismatrix im Vergleich zur Anpassung ohne Gewichtsfunktion – auch die Federlängenverteilung ändert sich in gewissem Umfang.
• Eine aufsteigende Iteration mit hohem Farbverlauf trägt zur Verbesserung der Anpassungsleistung bei.
• Es wird eine Verlaufsabstiegsiteration nr. 3 empfohlen.
• Die RDS-Qualität hat einen großen Einfluss auf die Anpassungsleistung.
• Wenn wir die RDS-Konsistenz sicherstellen können, kann eine Gewichtsfunktion die angepasste Matrix in die Nähe der wahren Matrix führen, von der aus das RDS abgeleitet worden wäre.